For ranking, ∆∆G alone is not great as it is dependent on number of atoms, while ligand efficiency (∆∆G over N_{heavy atoms}) alone favours molecules that are too small. So number of atoms needs to come into the equation.
For my ranking of compounds I have a weighted sum of ligand efficiency (negative good), RMSD from inspiration (low good), a penalty for number of new atoms added and a bonus for number of atoms.
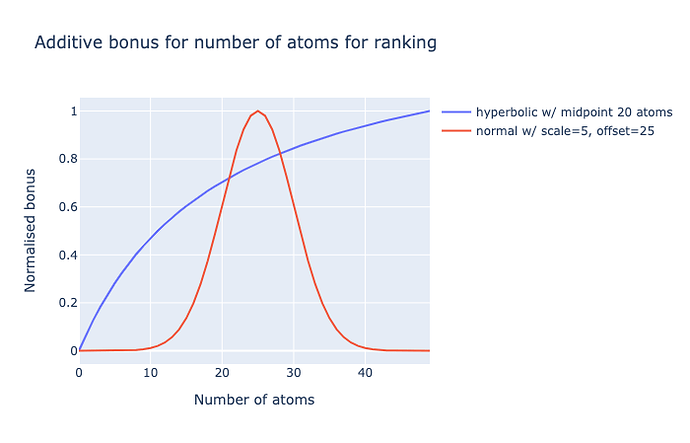
The latter is giving me trouble. Initially I had a rectangular hyperbola (like a Michalis-Menten curve) with midpoint 20 atoms (~240 Da), but this did not penalise large molecules.
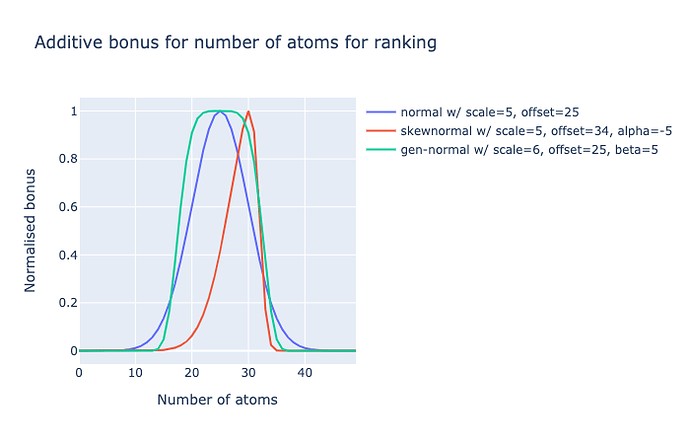
A normal distribution is a better option, but has issues:
Namely, it need to have more of a plateau (negative kurtosis), ie. diminishing returns on increasing number of atoms closer to the chosen median. So I am considering a generalised normal distribution for this. So anything with 20-30 atoms (240-360 Da) gets similar scores.
Alternatively, the left slope does rise steeply and maybe I would want to strongly penalise 500+ Da molecules (i.e. Lipinski rule), but penalise less <250 Da molecules, so a left-skew could an option.
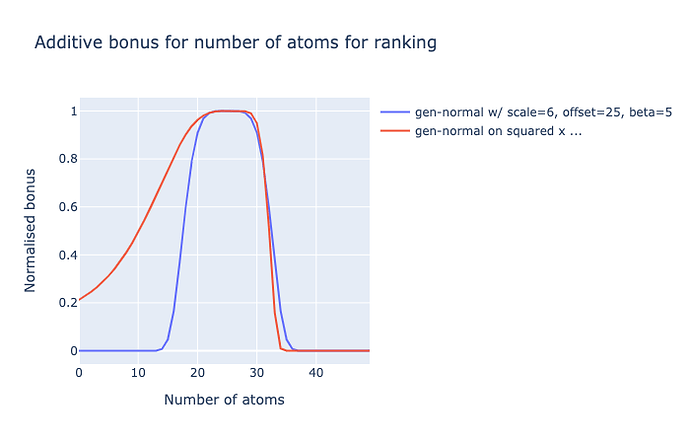
I could go beyond a generised normal distribution or a skew-normal, by monotonically distorting the values in a fudgey way, say squared:
I naïvely tried using skew_pdf(x, α) = 2 * normal_pdf(x) * normal_cdf(α * x) but with the generised normal, but gives odd results. I empirically opted for square of pre-scaled+offset, because power/exponential of x (like a log-normal) was also weird.
Getting the distribution of approved drugs does not seem like a great idea as many are small with broad specificity (e.g. valproate and aspirin are 180 Da), so arbitrarily distribution it is.
Questions
But the questions remain:
- which and what may best?
- what should be the cutoffs?
- and I suppose what should the weight for LE and this bonus be?
The answers are likely guesses and personal opinion based, but an informed guess is better than none in most cases.
Py code sandpit
import plotly.graph_objects as go
import numpy as np
from scipy.stats import skewnorm, gennorm
from scipy.special import erf
x = np.arange(50)
# rect hyperbola
current = x/(20+x)
norm = skewnorm.pdf((x - 25)/5, 0)
skn = skewnorm.pdf((x - 32)/5, -5)
mskn = skn1 / (0.1 + skn1)
ζ = (x - 25)/8
gnn = gennorm.pdf(ζ, 5)
# skew alla skew normal...
ζ = (x - 25)/16
gnn2 = gennorm.pdf(ζ, 5) * gennorm.cdf(2 * ζ, 5)
# skew by distortion of x
s = 2
ζ = (x**s - 25**s)/500
# ζ = (np.power(1.1, x) - np.power(1.1, 26))/10
gnn1 = gennorm.pdf(µ, 5)
def normalise(y):
y -= np.nanmin(y)
y /= np.nanmax(y)
return y
fig = go.Figure(data=[
go.Scatter(x=x, y=normalise(current), name='hyperbolic w/ midpoint 20 atoms'),
#go.Scatter(x=x, y=normalise(norm), name='normal w/ scale=5, offset=25'),
#go.Scatter(x=x, y=normalise(skn), name='skewnormal w/ scale=20, offset=20, alpha=-5'),
#go.Scatter(x=x, y=normalise(skn1), name='skewnormal w/ scale=5, offset=34, alpha=-5'),
#go.Scatter(x=x, y=normalise(skn1**.1), name='10th root of skewnormal w/ scale=5, offset=34, alpha=-5'),
go.Scatter(x=x, y=normalise(gnn), name='gen-normal w/ scale=6, offset=25, beta=5'),
go.Scatter(x=x, y=normalise(gnn1), name='gen-normal on squared x w/ scale=0.3, offset=25, beta=5'),
#go.Scatter(x=x, y=normalise(gnn2), name='gen-normal on squared x w/ scale=0.3, offset=25, beta=5'),
#go.Scatter(x=x, y=normalise(mskn), name='skewnormal w/ scale=8, offset=20, alpha=3')
],
layout=dict(title='Additive bonus for number of atoms for ranking',
xaxis={'title': 'Number of atoms'},
yaxis={'title': 'Normalised bonus'}))
fig.show()